Nonparametric causal effects based on incremental propensity score interventions を読んだ

要約(自分が読めたところだけ)

propensity scoreのオッズ比が$\delta$倍になるように介入確率を変化させるincremental propensity score intervention¹を提案。介入が二値変数でlongitudinal data²を扱う因果推論の問題において(1)positivityの仮定が不要で、(2)parametricな仮定を必要としない推定手法を提案。

著者によりRパッケージも公開されている。

設定

時刻$t=1,2,\ldots,T$に渡って以下のようなデータが得られている状況を考える。

• $\mathbf{Z}=(\mathbf{X}_1, A_1, \mathbf{X}_2, A_2,\dots,\mathbf{X}_T,A_T,Y)$: データ
• $\mathbf{X}_t$: 共変量
• $A_t$: 介入
• $Y$: アウトカム

incremental propensity score

観察データの時刻$t$におけるpropensity score$\pi_t(\mathbf{h}_t):=\mathbb{P}(A_t=1\mid\mathbf{H}_t=\mathbf{h}_t)$としたときに³、

\[q_t(\mathbf{h}_t;\delta,\pi_t) = \frac{\delta\pi_t}{\delta\pi_t+1-\pi_t}\]

をincremental propensity scoreとして定義する。計算するとわかるが、odds($\pi_t/(1-\pi_t)$)がちょうど$\delta$倍になるようなpropensity scoreになっている。 例えば、$\delta=1.5$のとき、$\pi_t(\dots)=0.5$の人は$q_t(\dots)=0.6$となり、$\pi_t(\dots)=0.05$の人は$q_t(\dots)=0.73..$となる。このように、incremental propensity scoreはpropensity scoreよりoddsが$\delta$倍になるようなものなので、人によって介入確率の変化は異なることがわかる。

理論パート

ちゃんと読めていないので省略。3章, 4章で議論されている。介入のoddsが$\delta$倍になった場合のincremental effect$\psi(\delta):=\mathbb{E}[Y^{\mathbf{Q(\delta)}}]$⁴がpositivityの仮定なしに観察データの分布についてのある量の期待値として識別可能ことや、推定手法の漸近性(Gauss仮定の弱収束すること)などが示されている。

提案手法

複雑かつ論文を読んだほうが正確なので省略。詳細は4章のAlgorithm1を参照。データを$K$分割して影響関数$\varphi$⁵の経験平均K個の平均を取る。$\varphi$の部分はカーネル法, スプライン, Boosting、ランダムフォレストなどなどの手法で推定する。

\[\hat{\psi}(\delta)=\frac{1}{K} \sum_{k=1}^{K} \mathbb{P}_{n}^{k}\left\{\varphi\left(\mathbf{Z} ; \hat{\boldsymbol{\eta}}_{-k}, \delta\right)\right\}=\mathbb{P}_{n}\left\{\varphi\left(\mathbf{Z} ; \hat{\boldsymbol{\eta}}_{-S}, \delta\right)\right\}\]

実験パート

シミュレーション

以下の式に従うデータを生成³。incremental treatment effectの真値とのbiasとRMSEを既存手法と比較している。局外パラメータの推定について、CorがCorrect ModelのときでMisがMisspesified Modelのとき、PはParametric、NPはNonparametricの場合を表している。概ねの設定で既存手法より良いか同等で、特にMisspecifiedでNonparametricな状況で既存手法よりも良い性能を達成している。

\[\begin{array}{l} &\left(X_{1}, X_{2}, X_{3}, X_{4}\right) \sim N(\mathbf{0}, \mathbf{I}) \\ &\mathbb{P}(A=1 \mid \mathbf{X})=\operatorname{expit}\left(-X_{1}+0.5 X_{2}-0.25 X_{3}-0.1 X_{4}\right) \\ &(Y \mid \mathbf{X}, A) \sim N\{\mu(\mathbf{X}, A), 1\}\\ &\mu(\mathbf{x}, a)=200+a\left\{10+13.7\left(2 x_{1}+x_{2}+x_{3}+x_{4}\right)\right\} \end{array}\]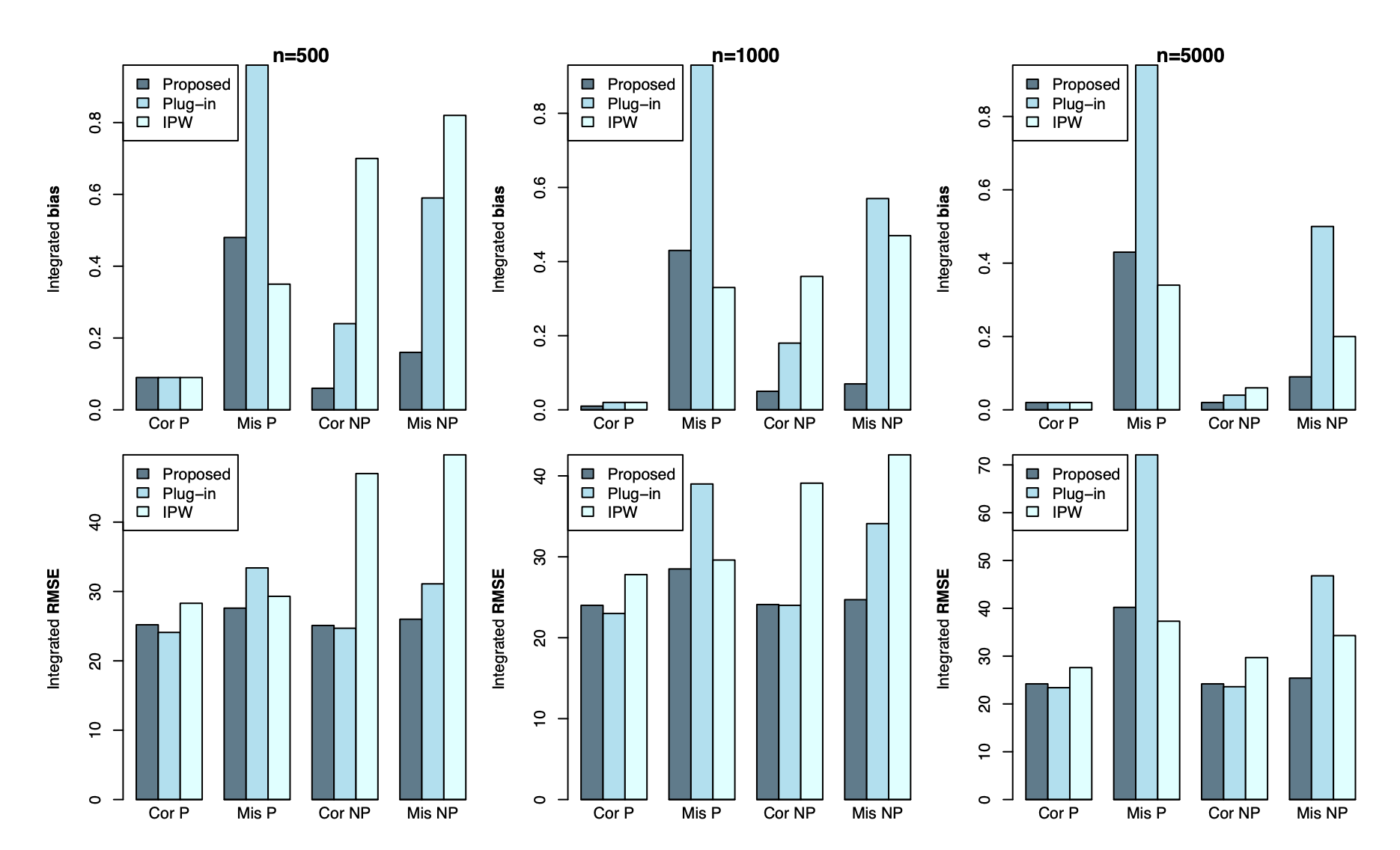

シミュレーションによる既存手法との比較

実データ

服役が結婚率に与える影響を調査したデータ(2001年から2010年, 4781人対象)を使って、提案手法でincremental treatment effectを推定した(下図)。$\delta=1$が観察結果で、各調査対象の服役のoddsがそこから$\delta$倍になったときの結婚率の変化を表している。服役のoddsが増加すると結婚率が下がっていることがわかる。

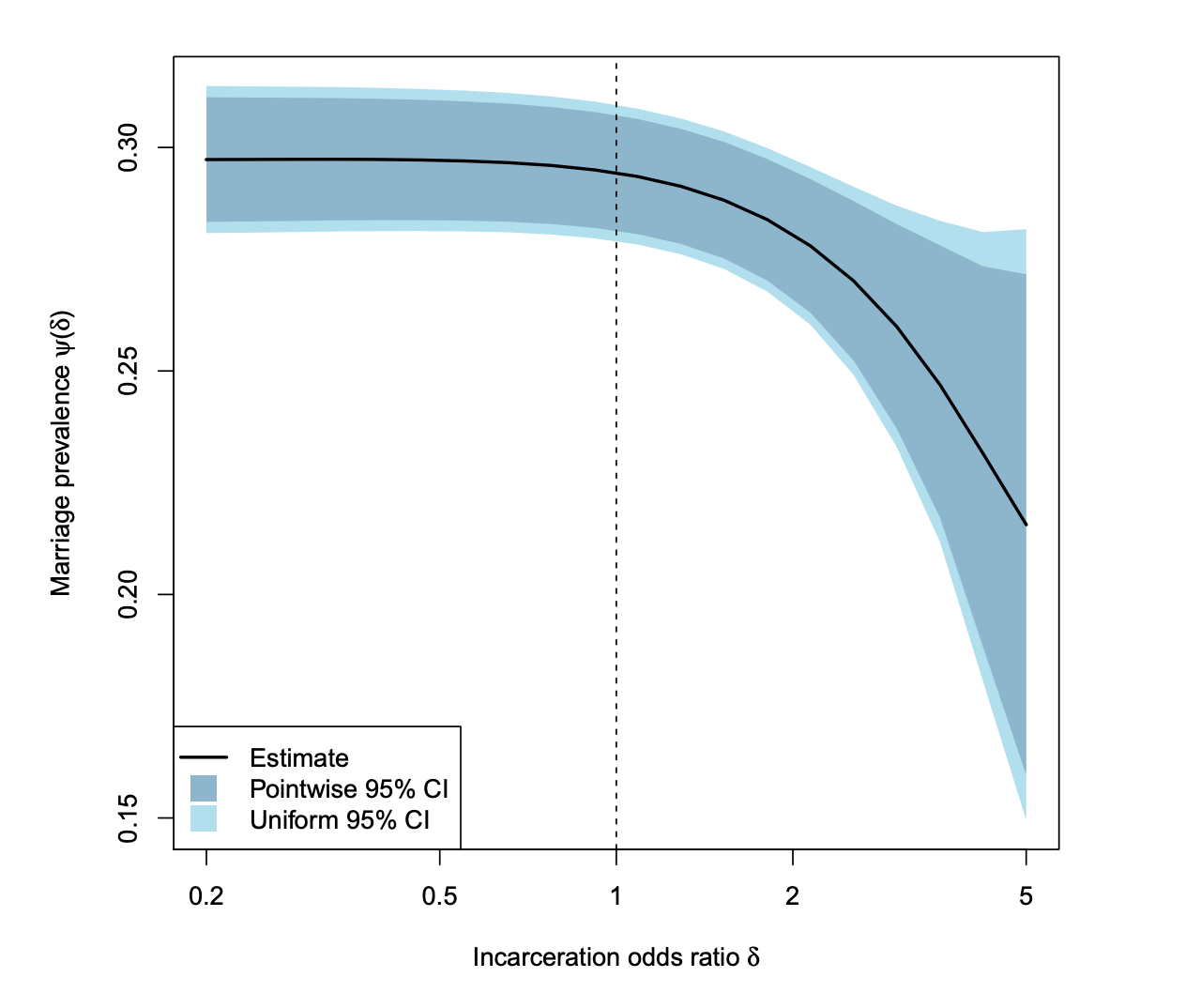服役のoddsの変化に対する結婚率の変化

参考文献

• Nonparametric causal effects based on incremental propensity score interventions

1. stochastic dynamic interventionという分類になるらしい。介入が確率的か決定的かでstochastic, determinitic、介入のルールが各時点で異なるか同じかでstatic, dynamicと呼び分けられているっぽい。 ↩

2. 同一の対象から異なる刻々の時点で繰り返し集められたデータのこと。政府の日英統計用語集をみると、縦断的データと訳されるようである。 ↩

3. このシミュレーションの設定はpropensity scoreの推定が不安定になる例として知られているらしい。詳しくは論文参照。 ↩ ↩²

4. $\mathbb{Q}$はstochastic interventionの列を表す。時刻$T$までの介入がincremental interventionの分布に従った場合の期待値を取っている。$Q_t\sim q_t(A_t\mid\mathbf{h}_t;\delta)$で抽出したとき、$\mathbf{Q}(\delta)=(Q_1,Q_2,\dots,Q_T)$と置いている。 ↩

5. 影響関数は方向微分みたいなもの。この場合の影響関数がどう定義されるのか、よくわかっていない。 ↩