Implicit Neural Representations with Periodic Activation Functions を読んだ
どんな論文？
高次の微分を含む陰関数方程式(implicit problem)を解く問題に対して活性化関数を$\sin$ 関数にしたNN(SIREN; sinusoidal representation network)を用いる手法を提案した。画像・動画・3D形状・音声など様々な領域の信号復元の問題がこの形式で定式化できて、各ドメインで信号復元の問題を解かせたところ、 既存のReLUなどを用いたNNに比べSNPR(Peak signale-to-noise ratio)が大幅に改善した。また、SIRENの適切な初期化条件についても理論・実験の両面から検証されている。
参考動画
implicit problemとは？
implicit problem
implicit problem とは 関数 $\Phi: \mathbb{R}^k \to\Omega$ で
$$
F(\boldsymbol{x}, \Phi, \nabla_{\boldsymbol{x}}, \nabla_{\boldsymbol{x}}^2\Phi, ...) = 0
$$
を満たすような関数を探す問題のこと。$\Omega\subset \mathbb{R}^l$ は適当な閉領域 ($\Omega = \bigcup_{m=1}^{M} \Omega_m$ みたいな感じで分割されていても良い)
SIRENの性質
SIREN
$$
\begin{align}
\mathrm{SIREN}_n(\boldsymbol{x}) & = \boldsymbol{W}_n(\phi_{n-1}\circ\phi_{n-2}\circ\cdots\circ\phi_0)(\boldsymbol{x})+\boldsymbol{b}_n \\
\phi_i & = \sin(\boldsymbol{W}_i\boldsymbol{x}+\boldsymbol{b}_i)
\end{align}
$$
つまり、アフィン変換と周期関数(\sin)を交互に繰り返す構造。
SIRENの導関数はSIRENの積
$\sin^\prime(\theta)=\cos(\theta)=\sin(\theta+\pi/2)$が成り立つので、導関数を計算すると各要素はSIRENの積になる。
例えば、1次元かつ$n=2$のSIRENの導関数を考えると
\[\begin{align} \mathrm{SIREN}_2(x) & = w_2\sin(w_1\sin(w_0x+b_0)+b_1)+b_2\\ \frac{d}{dx}\mathrm{SIREN}_2(x) & = w_2\sin^\prime(w_1\sin(w_0x+b_0)+b_1)\sin^\prime(w_0x+b_0))w_0 \\ & = w_2\sin(w_1\sin(w_0x+b_0)+b_1+\pi/2)\sin(w_0x+b_0+\pi/2)w_0 \end{align}\]となって、SIRENの積で評価できる。
論文では$n=5$としているらしい。
論文では各層で出力の分布が保たれるような初期化の方法についても議論していて、次の定理が成り立つ。
SIRENの初期化条件について
各重み成分を$\boldsymbol{W}_{ij}$とするとき$\boldsymbol{W}_{ij}\overset{i.i.d.}{\sim} \mathcal{U}(-\sqrt{6/\text{前層の入力数}},\sqrt{6/\text{前層の入力数}})$とすると、各層(2層目以降)の中間層の出力が標準正規分布に従う。
この初期化の方法により、出力の分布が層数によらないようにしている。実験も行われており、たしかに分布が変化していないことがわかる。
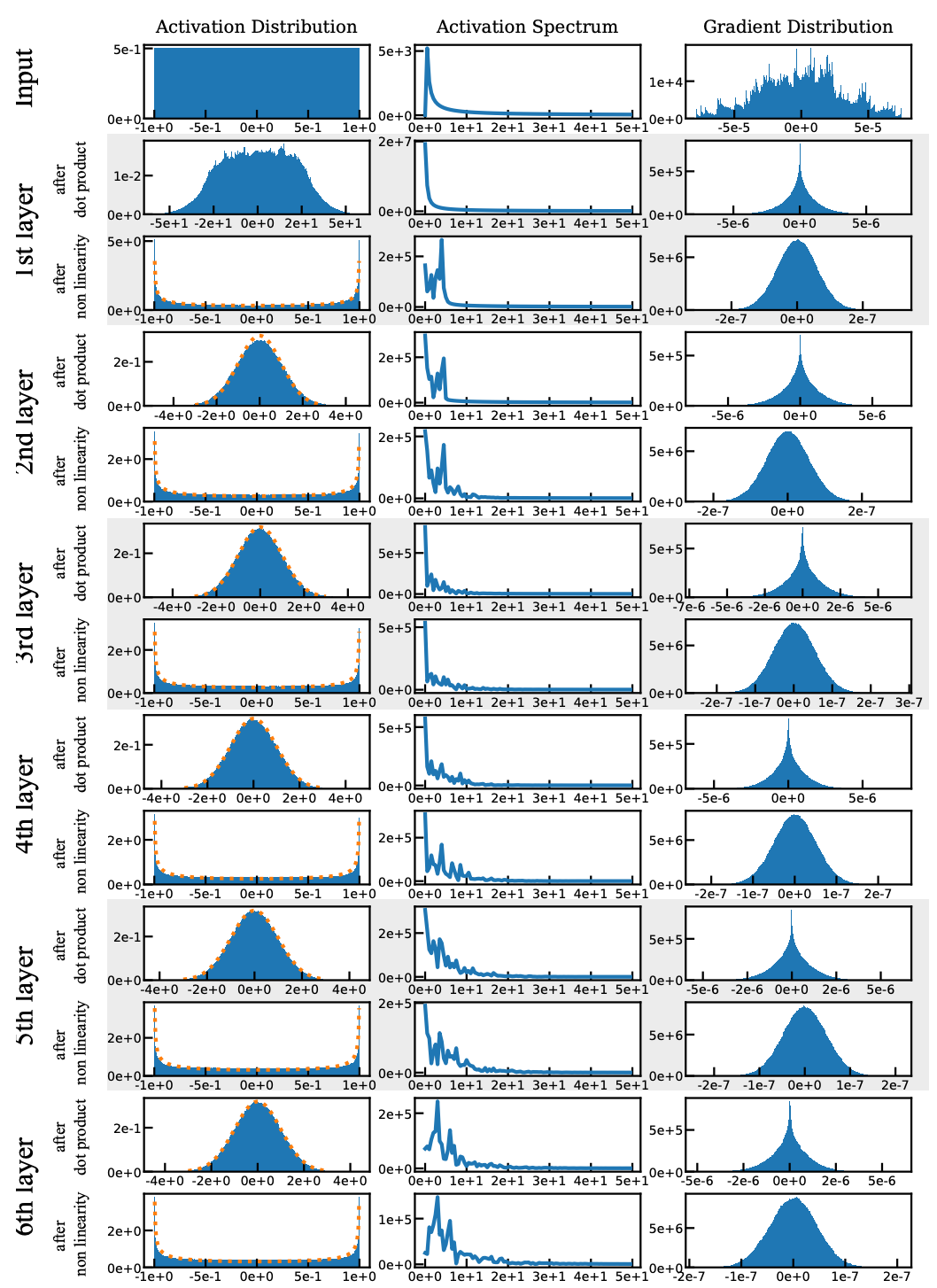6層のSIRENを上記の条件で初期化した場合の各層の分布とスペクトル。理論値と合致しており、スペクトルについても緩やかに変化していることが見て取れる。